Software and materials within this website are associated to the following paper:
This work focuses on those supervised tasks that are presented with a numerical output but decisions have to be made in a discrete, binarised, way, according to a particular cutoff. In other words, we have a training dataset as if we were facing a regression task but we have a deployment situation that is a binary classification task. Our proposed approach is easily understood by means of a real life example:
An estate agent has a database of possible customers who are interested in buying a house. The estate agent collects information about each customer and learns a model about the maximum mortgage that the customer can get from a bank. This is our regression model. On an everyday basis, several new properties enter the estate agent's portfolio. Each of them has a different price. Obviously, the estate agent only offers a property to those customers that can afford it, i.e., those that can get a mortgage for at least the property price. That means that each property represents a genuine cutoff in our binarisation setting.
This binarised regression task is a very common situation that requires its own analysis, being this analysis different from regression and classification -and ordinal regression. How to address this task and how should it be evaluated are two of the main questions that this work deals with.
Context plots and Cutoff Distributions for the Binarised Regression problems can be found here.
The basic idea arising the Binarised Regression problems is that, for many applications, we are interested in telling whether the predictions are above or below a given cutoff. This cutoff c can vary depending on the context and will critically determine the overall performance.
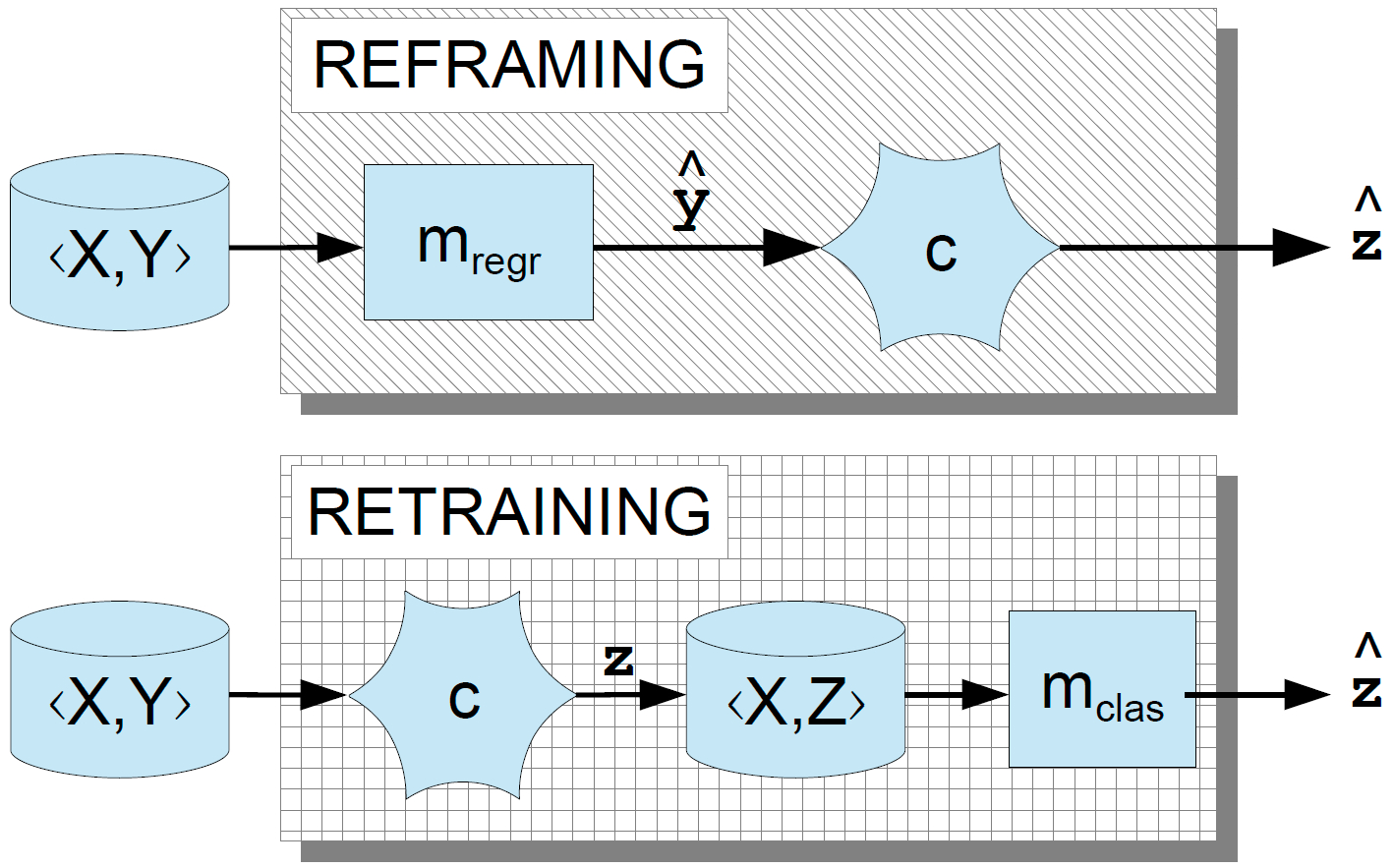
We study two basic approaches to address this task:

A comprehensive evaluation of the retraining and reframing approaches is performed in this work. Using the newly introduced plots for spotting the regions in which one technique dominates over the other allows us to discard approaches that are suboptimal for every possible operating context.
Up to 20 datasets from different repositories are presented as binarised regression problems, showing that these are common situations in many research fields.
Any use of this software (even non-profit or academic uses) should be done only after contacting the authors first (signature at the bottom part). We will most probably grant permission to use it freely and even point to newer versions if there are.
A running example using real mortgages data from Zillow (Zillow API 2013(*)) and real cutoffs from the US Federal Financial Institutions Examination Council (Federal Financial Institutions Examination Council: Home Mortgage Disclosure Act, HMDA 2013) is used throughout the paper. This is a prototypical case of a binarised regression problem where the distributions for the output values and for the cutoffs are similar, as the next figure shows.
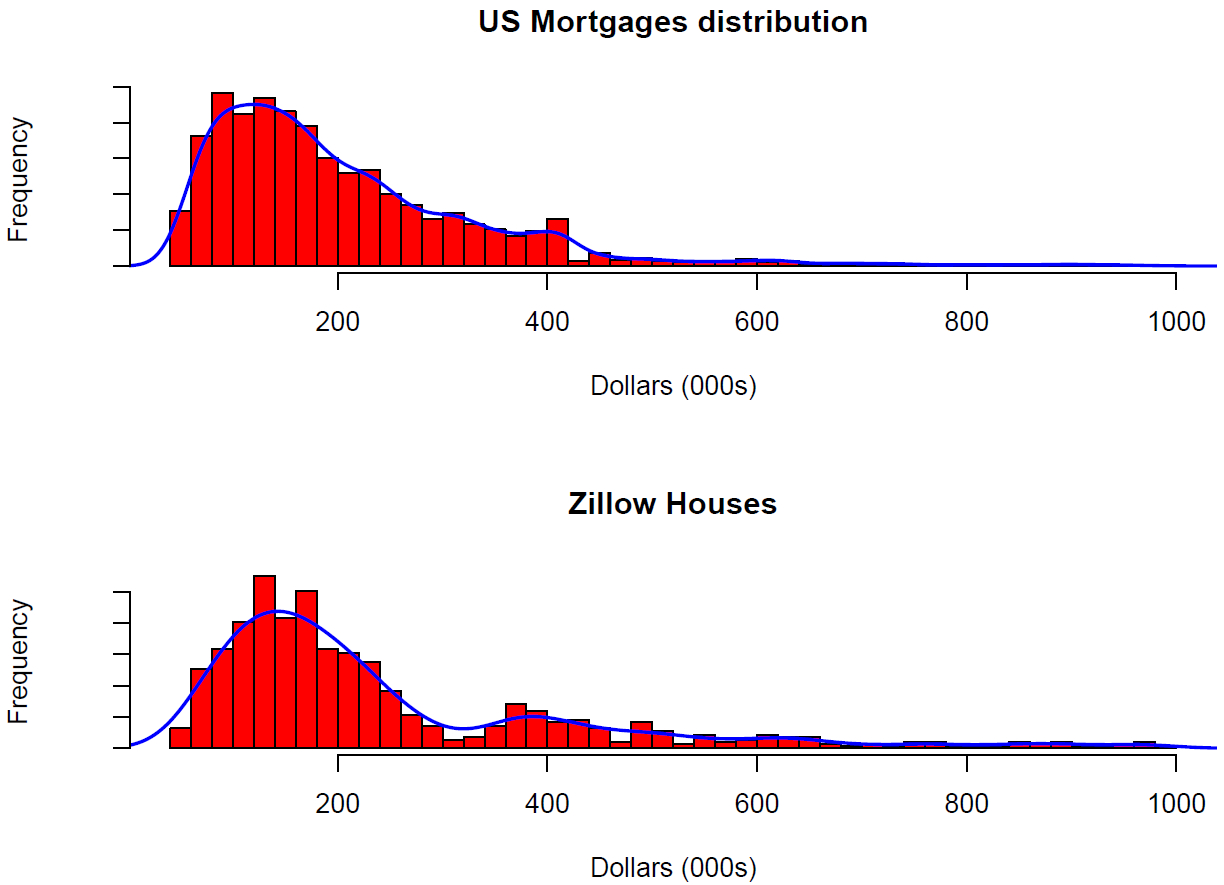
As stated in Context plots and Cutoff Distributions for the Binarised Regression problems, this example belongs to case B, is of typology 3 and corresponds to a 'supply-demand regulation' case.
Note (*): Zillow data have partially been anonymised.